Introducción
La graficación de ecuaciones es un recurso necesario para comprender con mayor facilidad diversas ideas matemáticas. Su aprendizaje inicia en la secundaria, se continúa en la preparatoria y se utiliza intensivamente en los estudios de licenciatura en las diferentes áreas académicas; por esta razón, es importante conocer el uso de esta herramienta para interpretar diversos conceptos como el de función matemática y manejar correctamente sus diferentes representaciones gráficas.
El método más común de hacer la gráfica de una ecuación es la representación cartesiana en un sistema de ejes coordenados; esta metodología fue desarrollada en el siglo XVI por René Descartes, a quien se considera como el creador de la geometría analítica. Sin embargo, es justo mencionar que en la matemática se han desarrollado otros sistemas de referencia para la representación gráfica de ecuaciones; la conveniencia de cada uno de ellos depende de la naturaleza y tipo de problema que se aborde y de la dimensión espacial en que se confina (en un plano o en el espacio tridimensional).
El tema que estudiarás a continuación se enfoca en el uso del método cartesiano en el plano, ya que es ampliamente utilizado, tiene aplicación directa a la geometría y facilita la transición a otros tipos de sistemas coordenados.
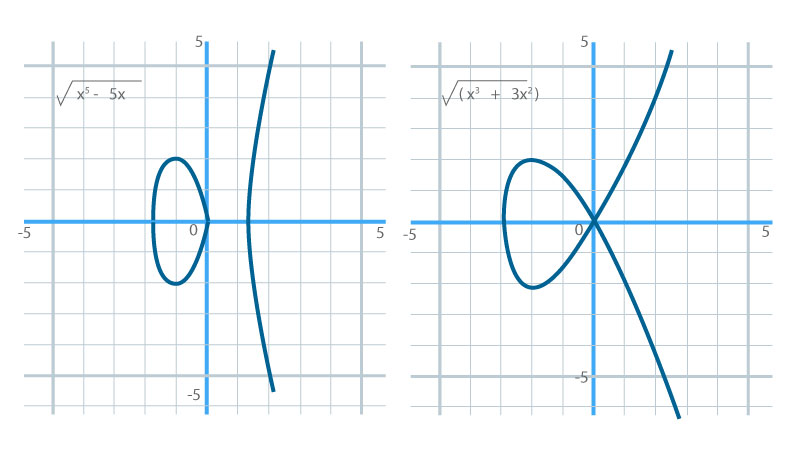
Ejemplo de curva plana