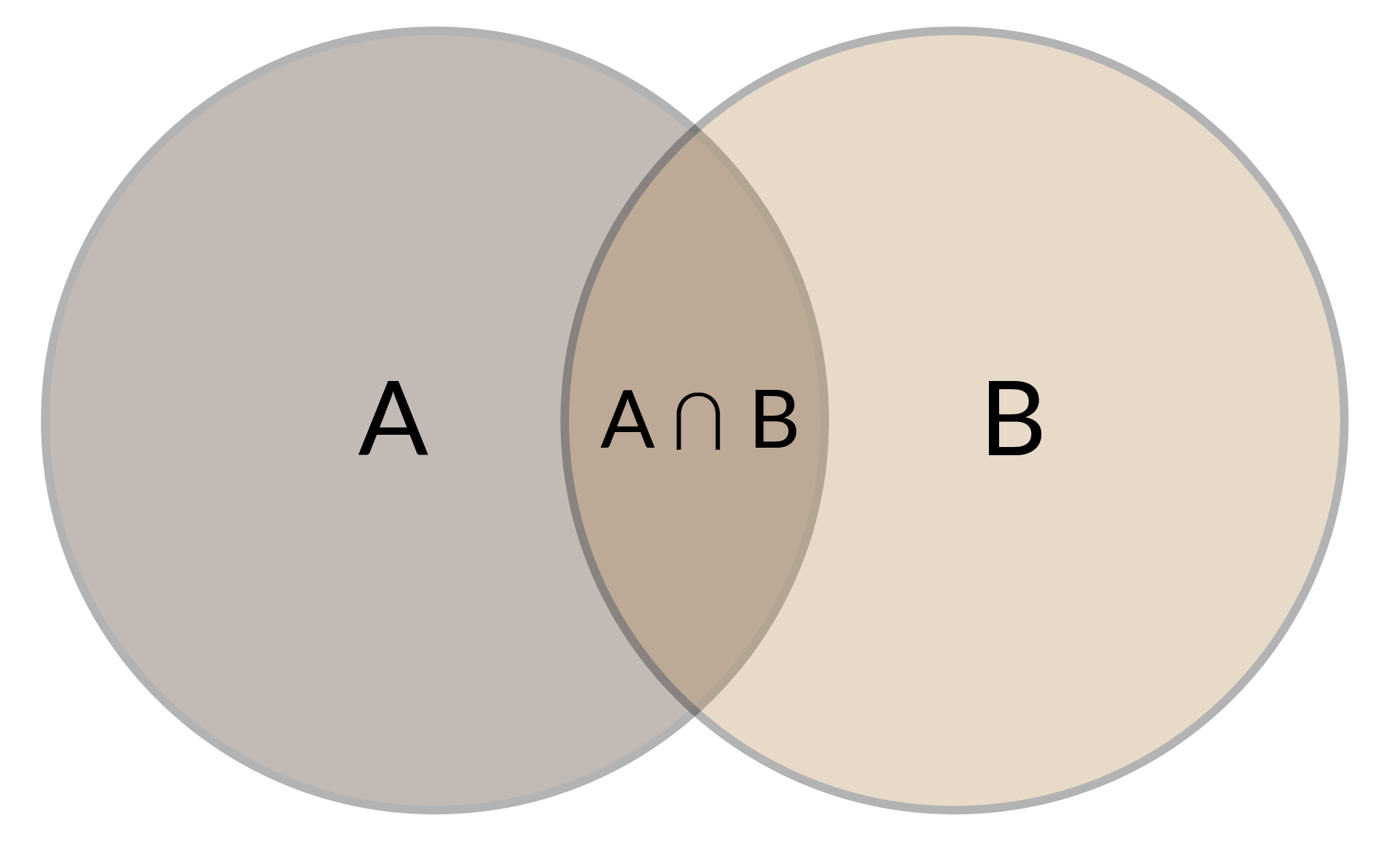
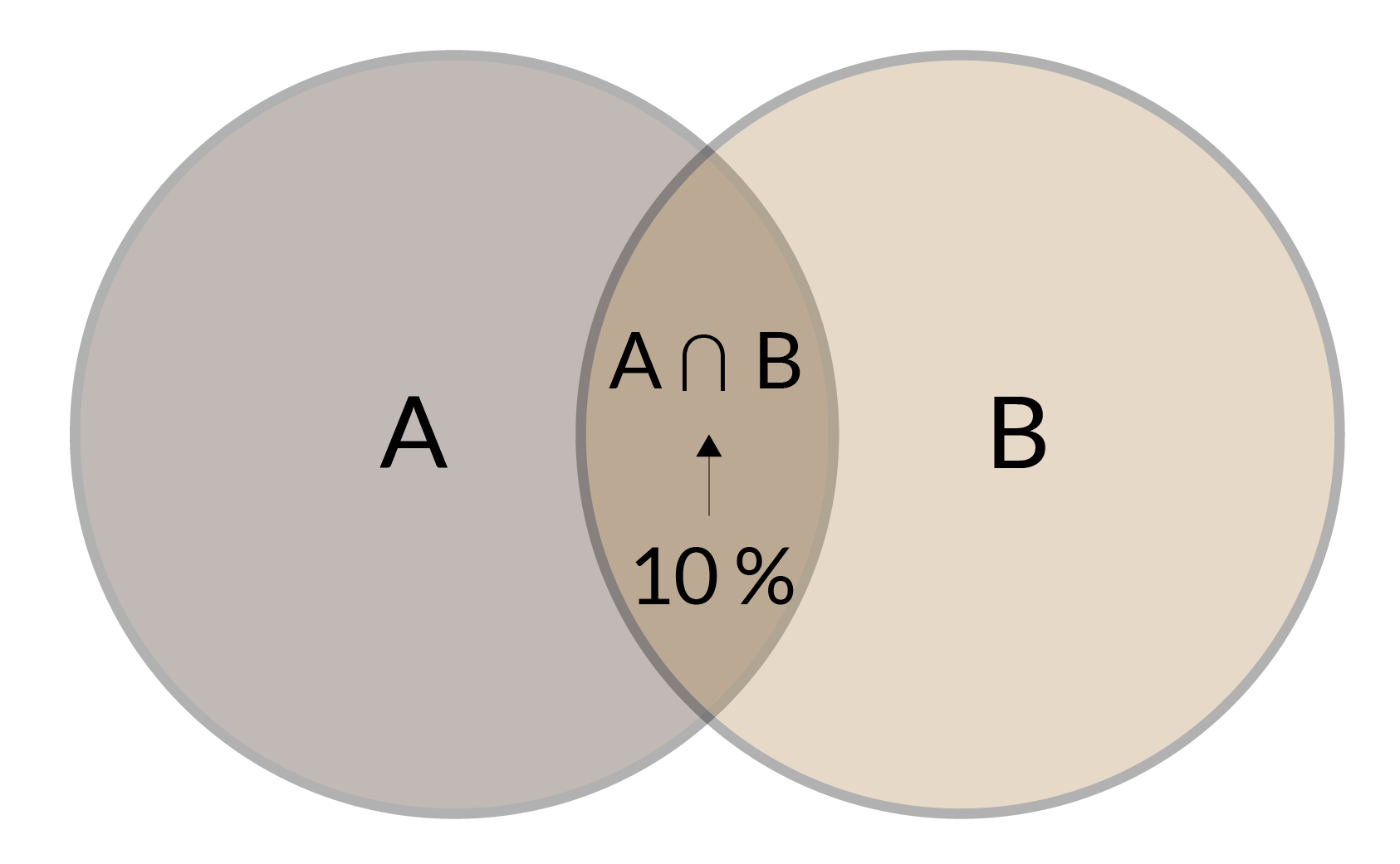
Introducción
La probabilidad es una rama de las matemáticas, cuyo desarrollo tiene origen en el siglo XVII, cuando se buscó contar con métodos racionales para enfrentar los juegos de azar. Se puede decir que hay tres grandes enfoques, escuelas o paradigmas de probabilidad, a saber, el clásico, el empírico y el subjetivo, ninguno de los cuales escapa al tratamiento axiomático, el cual da la estructura al tratamiento matemático moderno de la probabilidad.
A la probabilidad clásica también se le conoce como a priori. Se basa en el hecho de que al momento de realizar un experimento aleatorio se obtendrá un resultado cualquiera, sin poder determinar su naturaleza.
La escuela empírica o frecuencial se fundamenta en el punto de vista de Aristóteles: “lo probable es aquello que ocurre diariamente”.
Por otra parte, la escuela subjetiva sostiene que la probabilidad de que ocurra un suceso se sustenta en la experiencia previa, en el punto de vista de algún observador o mediante la intuición.

(s. a) (2016). [Tirar los dados] [fotografía]. Recuperada de https://pixabay.com/es/tirar-los-dados-dados-juego-de-mesa-1502706/