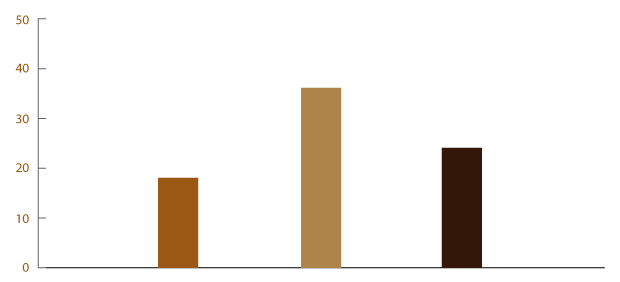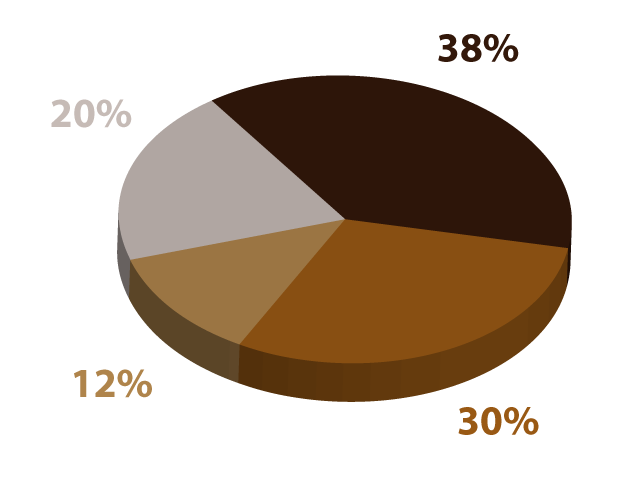Gráficas

Unidad de Apoyo para el Aprendizaje

Iniciar

Introducción


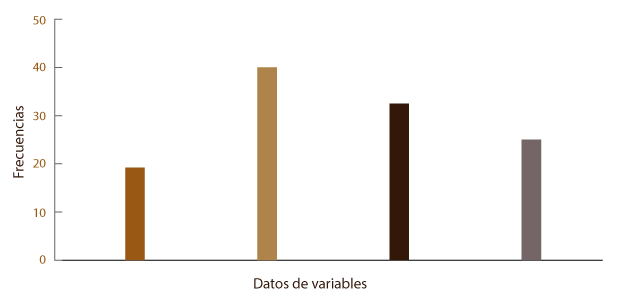
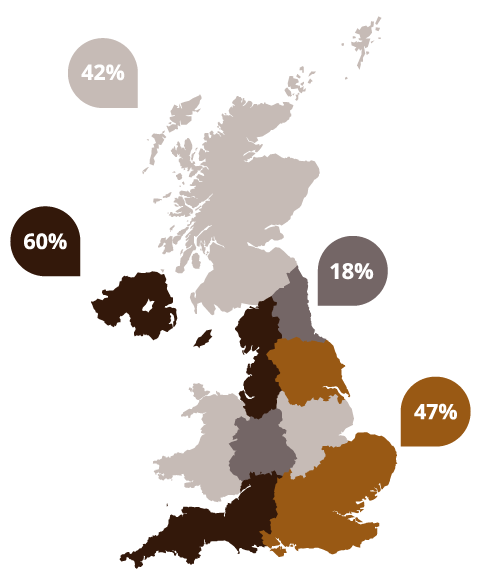
Un parte sustancial del análisis estadístico de datos son las gráficas. Lo anterior se debe a que los datos obtenidos a través de los diferentes métodos e instrumentos de recolección de información terminan visualmente con la presentación de algún tipo de gráfica.


Sin embargo, el uso de las gráficas no es trivial, ya que cada una de ellas representa mejor el valor que adquiere una variable después de darle tratamiento estadístico. En el presente tema, estaremos revisando los distintos tipos de gráficas que se utilizan, los pasos a seguir para la elaboración de algunas de ellas y su correcta aplicación.


Computadora portátil que muestra en pantalla diversos datos y representaciones gráficas de los mismos

Goumbik. (2017). Estadísticas [fotografía]. Tomada de https://pixabay.com/es/oficina-negocio-port%C3%A1til-2717014/

El estudio de este tema te permitirá:

Identificar las distintas herramientas gráficas en el manejo de datos estadísticos, a través de apoyos visuales y sus aplicaciones, para la correcta interpretación de la información y toma de decisiones.

Las gráficas permiten explicar más fácilmente el comportamiento de los datos en estudio, muestran, explican, interpretan y analizan de manera sencilla, clara y efectiva los datos estadísticos mediante formas geométricas como líneas, áreas, volúmenes, superficies, etc.; permiten, además, la comparación de magnitudes, tendencias y relaciones entre los valores que adquiere una variable.

Histogramas y polígonos de frecuencias


Un histograma de frecuencias es un gráfico de rectángulos que tiene su base en el eje de las abscisas —eje horizontal o de las x—, con anchura igual, cuando se trata de representar el comportamiento de una variable discreta y anchura proporcional a la longitud del intervalo, cuando se desea representar una variable continua. En este último caso, el punto central de la base de los rectángulos equivale al punto medio de cada clase.


Gráfico de barras mostrando la comparativa entre los diversos partidos y las elecciones del Parlamento Europeo en 1999 y 2004


Las alturas de los rectángulos ubicadas en el eje de las ordenadas — eje vertical o de las y — corresponde a las frecuencias de las clases. El área de los rectángulos así formados es proporcional a dichas frecuencias.

Pasos a seguir para la elaboración de un diagrama de frecuencias —o polígono de frecuencias— y un histograma.

Datos

Considera el siguiente conjunto de datos:


8.9 8.3 9.2 8.4 9.1
8.6 8.9 9.1 8.8 8.8
8.8 9.1 8.9 8.7 8.8
8.9 9.0 8.6 8.7 8.4
8.6 9.0 8.8 8.9 9.1
9.4 9.0 9.2 9.1 8.8
9.1 9.3 9.0 9.2 8.8
9.7 8.9 9.7 8.3 9.3
8.9 8.8 9.3 8.5 8.9
8.3 9.2 8.2 8.9 8.7
8.9 8.8 8.5 8.4 8.0
8.5 8.7 8.7 8.8 8.8
8.3 8.6 8.7 9.0 8.7
8.4 8.8 8.4 8.6 9.0
9.3 8.8 8.5 8.7 9.6
8.5 9.1 9.0 8.8 9.1
8.6 8.6 8.4 9.1 8.5
9.1 9.2 8.8 8.5 8.3
9.3 8.6 8.7 8.7 9.1
8.8 8.7 9.0 9.0 8.5
8.5 8.8 8.9 8.2 9.0
9.0 8.7 8.7 8.9 9.4
8.3 8.6 9.2 8.7 8.7
8.7 9.7 8.9 9.2 8.8
8.3 8.6 8.5 8.6 9.7
Máximo 9.7 9.7 9.7 9.2 9.2 = 9.7
Mínimo 8.3 8.3 8.2 8.2 8.0 = 8.0

Paso 1

Cuenta el número de datos en la población o muestra; en este caso, son 125 lecturas, por lo tanto, n= 125.


Paso 2

Calcula el rango de los datos (R). Para determinarlo, lo único que se debe hacer es encontrar el número mayor y el menor de las 125 lecturas que se tienen en la tabla. En este caso: máximo= 9.7; mínimo= 8.0. El rango (R) es la diferencia entre estos valores. Así: R= máximo – mínimo (9.7 - 8.0= 1.7).


Paso 3

Determina el número de clases, celdas o intervalos. En la construcción de un diagrama de frecuencias o de un histograma, es necesario encasillar las lecturas. El número de clases no debe ser menor de 6, ni mayor de 15. En este sentido, si Q es la cantidad de clases que tendrá el histograma; se recomienda lo siguiente:


Número de lecturas Número de clases
< 50 6 - 8
50 - 100 9 - 11
100 - 250 8 - 13
> 250 10 - 15

Paso 4

Determina el ancho C del intervalo. Para este caso, utilizamos la siguiente fórmula:


Fórmula para determinar el ancho del intervalo C; C=R/Q=1.7/10=0.17

(s. a.) (s. f.). Fórmula de C [tabla].


Generalmente, es necesario redondear C para trabajar con números más cómodos.


Paso 5

Establece los límites de clase. En muchos casos, esto sucede automáticamente y depende de la costumbre; por ejemplo, si se le pregunta su edad a una persona, ésta contestará con el número de años que tiene. En este caso, el ancho de clase es automáticamente de un año, aunque la persona haya cumplido años ayer o hace 11 meses. En otras instancias, la resolución en los instrumentos de medición es la que determina el ancho de clase, aun cuando es necesario dar una regla general que se mantenga para lograr una normalización del histograma. En el ejemplo, la lectura menor fue de 8.0 por lo que se podría tomar éste como el límite inferior de la primera clase y, al sumar al valor de 8.0 el ancho de clase C, se tendría el límite inferior del segundo intervalo y así sucesivamente hasta que todos los valores de la tabla queden contenidos.


Paso 6

Construye la distribución de frecuencias:


Clase Límite de clase Marca de clase Frecuencia Total
1 8.00-819 8.1 I 1
2 8.20-839 8.3 IIIIl IIII 9
3 8.40-859 8.5 IIIIl IIIlI I 16
4 8.60-879 8.7 IlIII IIlII IlIII IIIlI IIlII II 27
5 8.80-8.99 8.9 IlIII IIIlI IIIlI IIlII IIIlI IIlII I 31
6 9.00-9.19 9.1 IIlII IIIlI IlIII IIlII III 23
7 9.20-9.39 9.3 IIlII II 12
8 9.40-9.59 9.5 II 2
9 9.60-9.79 9.7 III 4
10 9.80-9.99 9.9 0
Suma de F= N = 125

(s. a.) (s. f.). Datos [tabla].


Paso 7

Al graficar los datos anteriores, obtenemos la siguiente figura:


Histograma de frecuencias, cuyo eje de las x va de 8.0 a 9.8 y el eje de las y de 0 a 40

(s. a.) (s. f.). Histograma de frecuencias [tabla].


La forma más habitual de representar la información contenida en una tabla es a partir de un sistema de ejes cartesianos.


Representación gráfica de distribuciones

Hay, no obstante, otras formas de representar datos. Para hacer más clara la exposición de las diferentes representaciones gráficas, distinguiremos las referentes a dos tipos de distribuciones:


Distribuciones sin agrupar
Distribuciones agrupadas en intervalos

Gráficas para distribuciones de frecuencias sin agrupar



Para representar este tipo de distribuciones, los gráficos más utilizados son:


Diagrama de barras

Se emplea para distribuciones tanto de variables estadísticas como de atributos.

Diagrama circular

Es el más comúnmente utilizado para distribución de atributos.

Cartograma y pictograma

Utilizados para representar distribuciones de frecuencia, a través de un icono o un mapa.

Diagrama en escalera

Empleado para frecuencias acumuladas.

Diagrama de barras


Es la más sencilla de las gráficas y consiste en representar datos mediante una barra o columna simple, la cual puede ser colocada horizontal o verticalmente.



A partir de este diagrama, es fácil darse cuenta de en qué valores de la variable se concentra la mayor parte de las observaciones.


Histograma de frecuencias de barra vertical mostrando tres datos, cuyas frecuencias son 15, 35 y 25

(s. a.) (s. f.). Diagrama de barras [tabla].


Una variante de este diagrama, tal vez más utilizada por ser más ilustrativa, es el diagrama de rectángulos; consiste en representar, en el eje de las abscisas, los valores de la variable y, en el de las ordenadas, las frecuencias; sobre cada valor de la variable, se levanta un rectángulo con base constante y altura proporcional a la frecuencia absoluta.


Histograma de frecuencias de rectángulos, cuyos valores de frecuencia son 30, 40, 35, 30

(s. a.) (s. f.). Diagrama de rectángulos [esquema].


Diagrama circular


Esta representación gráfica es especialmente adecuada en aquellos casos en que se desea que los datos estadísticos lleguen a todo tipo de persona, incluso a las que no tienen por qué tener una formación científica.


Paso 1


Se traza un círculo.

Paso 2


A continuación, se divide éste en tantas partes como componentes haya.

Paso 3


El tamaño de cada una de ellas será proporcional a la importancia relativa de cada componente.

Paso 4


En otras palabras, como el círculo tiene 360o, éstos se reparten proporcionalmente a las frecuencias absolutas de cada componente.

Resultado


Éste es el resultado.


Gráfica circular dividida en cuatro partes, los porcentajes son los siguientes: 38 %, 30 %, 20 % y 12 %

(s. a.) (s. f.). Gráfica circular [esquema].



Pictograma


Es otra forma de representar distribuciones de frecuencias. Consiste en tomar como unidad una silueta o un símbolo que sea representativo del fenómeno que se va a estudiar.


Dibujo de una casa a la cual se le atribuye el valor de 100 viviendas, seguido de un ejemplo de tres casas cuyo valor es de 300 viviendas

Cartograma


Son especialmente útiles en estudios de carácter geográfico. La forma de construirlos es la siguiente: se colorea o se raya con colores e intensidades diferentes los distintos espacios o zonas —que pueden ser comunidades autónomas, provincias, ríos, etc.—, en función de la mayor o menor importancia que tenga la variable o atributo en el estudio.


Mapa de Reino Unido con división política, rueda representando importaciones de neumáticos
Mapa de Reino Unido con división política, rueda representando importaciones de neumáticos

(s. a.) (s. f.). Cartograma de Reino Unido y neumático en importaciones [esquema].
Designed by Katemangostar / Freepik

Diagrama en escalera


Su nombre responde a que la representación tiene forma de escalera. Se utiliza para representar frecuencias acumuladas. Su construcción es similar a la del diagrama de barras; se elabora de la forma siguiente:

Elaboración

Paso 1


En el eje de las abscisas, se miden los valores de la variable o las modalidades del atributo; en el de las ordenadas, las frecuencias absolutas acumuladas.

Paso 2


Se levanta, sobre cada valor o modalidad, una barra, cuya altura es su frecuencia acumulada.

Paso 3


Por último, se unen mediante líneas horizontales cada frecuencia acumulada a la barra de la siguiente.

Paso 4


Los pasos anteriores conducen a la escalera; la última ordenada corresponderá al número total de observaciones.

Resultado


Finalmente, obtenemos una gráfica de este estilo:


Gráfica de escalera de forma ascendente que contempla tres valores: 20, 30 y 50

(s. a.) (s. f.). Diagrama en escalera [esquema].

Gráficas para distribuciones de frecuencias agrupadas en clases


Para distribuciones agrupadas en intervalos, existen básicamente tres tipos de representaciones gráficas: el histograma, el polígono de frecuencias y las ojivas.


Polígono de frecuencias


Es un gráfico de línea que se construye sobre el sistema de coordenadas cartesianas, al colocar sobre cada marca de clase, un punto a la altura de la frecuencia asociada a esa clase; posteriormente, estos puntos se unen por segmentos de recta. Para que el polígono quede cerrado, se debe considerar un intervalo más al inicio y otro al final con frecuencias cero.


Gráfica de un polígono de frecuencia, cuyos puntos son 20, 30, 45, 30, 25 y 10

(s. a.) (s. f.). Polígono de frecuencias [esquema].


Ojivas


Si en lugar de frecuencias absolutas utilizamos las acumuladas, obtendremos, en vez del histograma, una representación gráfica en forma de línea creciente que se conoce con el nombre de ojiva.


La ojiva es el polígono que se obtiene al unir por segmentos de recta los puntos situados a una altura igual a la frecuencia acumulada, a partir de la marca de clase, en la misma forma en que se realizó el polígono de frecuencias. La ojiva también es un polígono que se puede construir con la frecuencia acumulada relativa.


Gráfica de ojiva que parte del valor cero y aumenta en 10, 15, 45, circular dividida

(s. a.) (s. f.). Gráfica de ojiva [esquema].

Gráfica circular dividida

Gráfica de ojiva [esquema].

Con la revisión de las ojivas, se han revisado todas las gráficas que se utilizan para proporcionar de forma visual información, sin entrar a detalle en la información.

Actividad. Las gráficas y yo

Las gráficas son herramientas visuales que te permiten obtener, de manera inmediata, información sobre los datos estadísticos revisados; es importante que sepas que unas resultan mucho más prácticas que otras, por ello es que se vuelve necesario que sepas cuando debes usarlas.

Autoevaluación. Gráficas

Ahora que conoces las distintas gráficas y la forma adecuada en la que las puedes utilizar, así como el comportamiento de las variables y el tipo de información que están representando, te invitamos a que, con la información obtenida, reflexiones sobre el uso y aplicación de las mismas.


Fuentes de información

Básicas

Camargo, A., García, J., Minjares, M., Rodríguez, A. y Serrano, R. (2010). Gráfica de datos. Estadística I. Licenciatura en Contaduría [CD-ROM]. Ciudad de México: Universidad Nacional Autónoma de México.


Complementarias

Levine, D. M., Krehbiel, T. C. y Berenson, M. L. (2001). Estadística para administración (2.ª ed.). Ciudad de México: Prentice Hall.


Levin, R. I. y Rubin, D. S. (2004). Estadística para administración y economía (7.ª ed.). Ciudad de México: Pearson Educación.