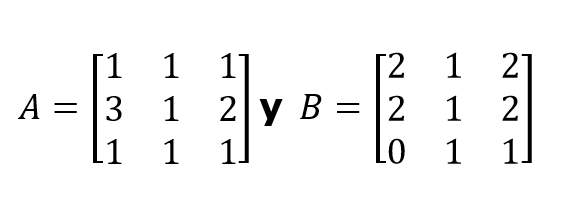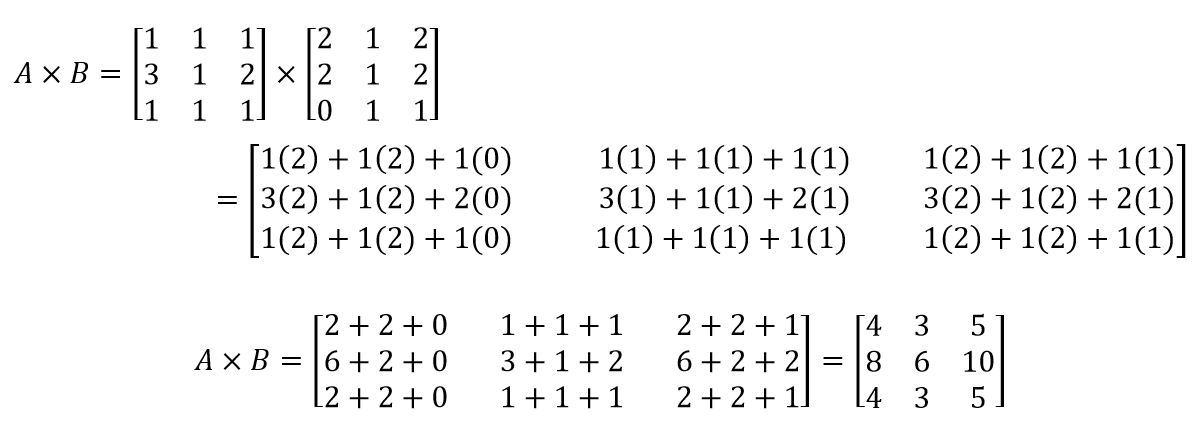Introducción
Las matrices son una herramienta muy útil para expresar y discutir problemas que surgen en la vida real. En los negocios, a menudo se necesita calcular y combinar ciertos costos y cantidades de productos, lo cual normalmente se expresa a través de tabulaciones; sin embargo, esta capacidad de visualización no siempre rinde en una mecanización que permita desarrollar métodos de análisis.
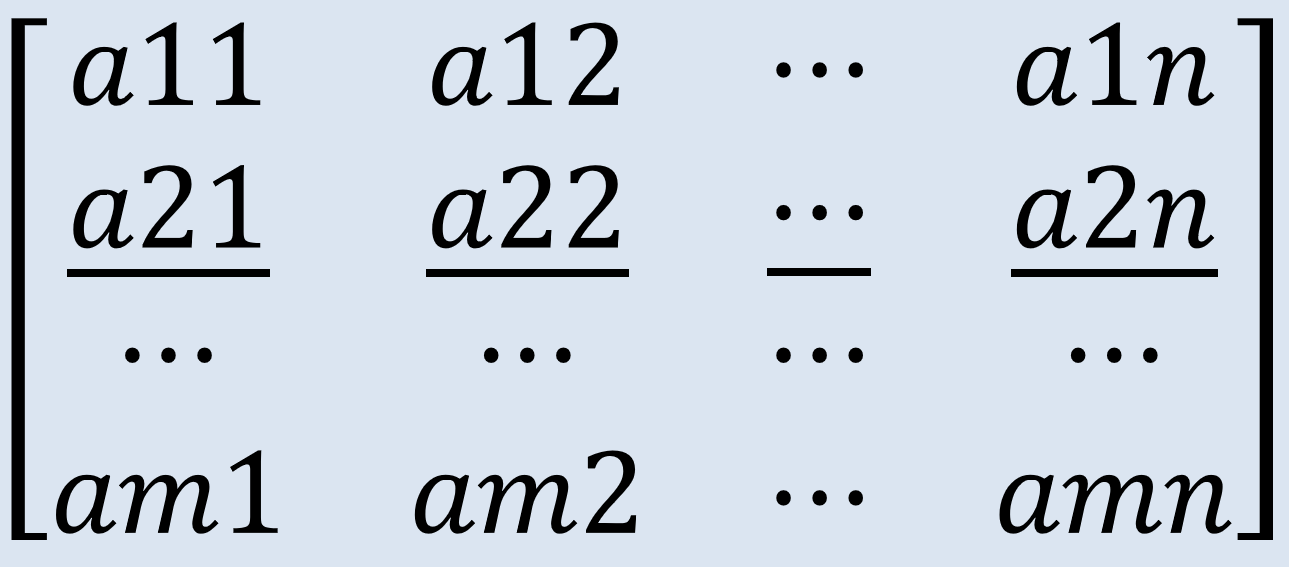
Afortunadamente, para estas situaciones existe una metodología matemática más clara, fácil y rápida de operar, la cual se denomina matriz.
Un ejemplo del uso de matrices lo representa Internet, donde los motores de búsqueda para localización y recuperación de información las utilizan para seguir el rastro de las ubicaciones donde dicha información se encuentra, así como su tipo de acuerdo con el criterio de búsqueda y las palabras clave e incluso para determinar la manera en que los sitios web se vinculan entre sí.
También se pueden modelar “humanamente” con una tabulación o conjuntos de ellas; sin embargo, para realizar las búsquedas de manera ágil, se debe recurrir a los métodos que ofrece el álgebra lineal, lo cual facilita la conformación y operación de estas estructuras. La pertinencia de estas metodologías estriba en la capacidad de representar y manejar todo el problema y establecer su solución algorítmica por medio del lenguaje matemático.
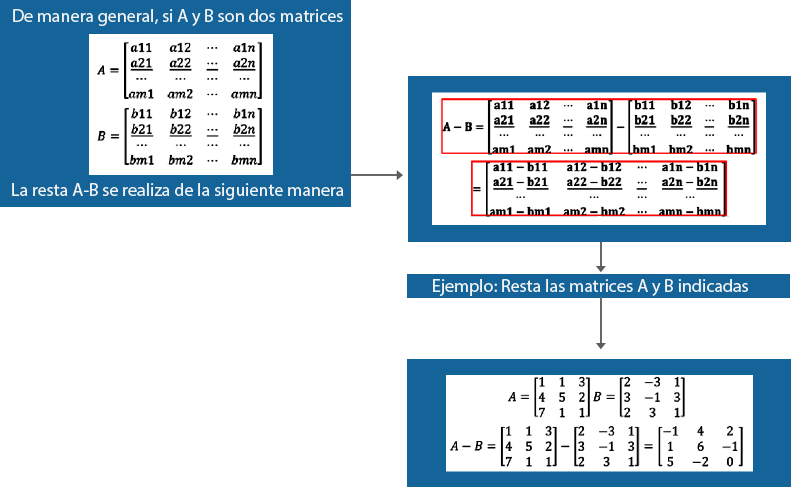
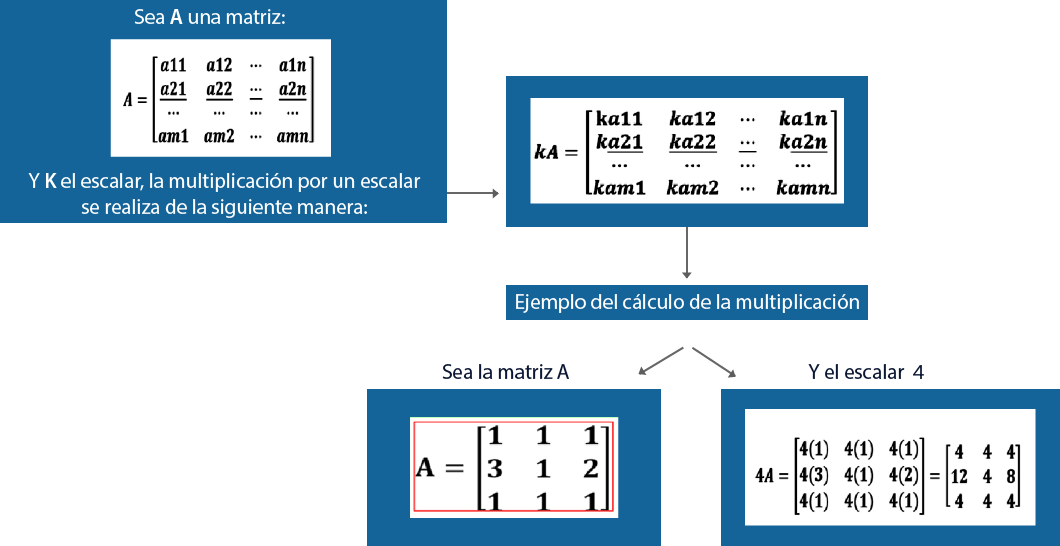
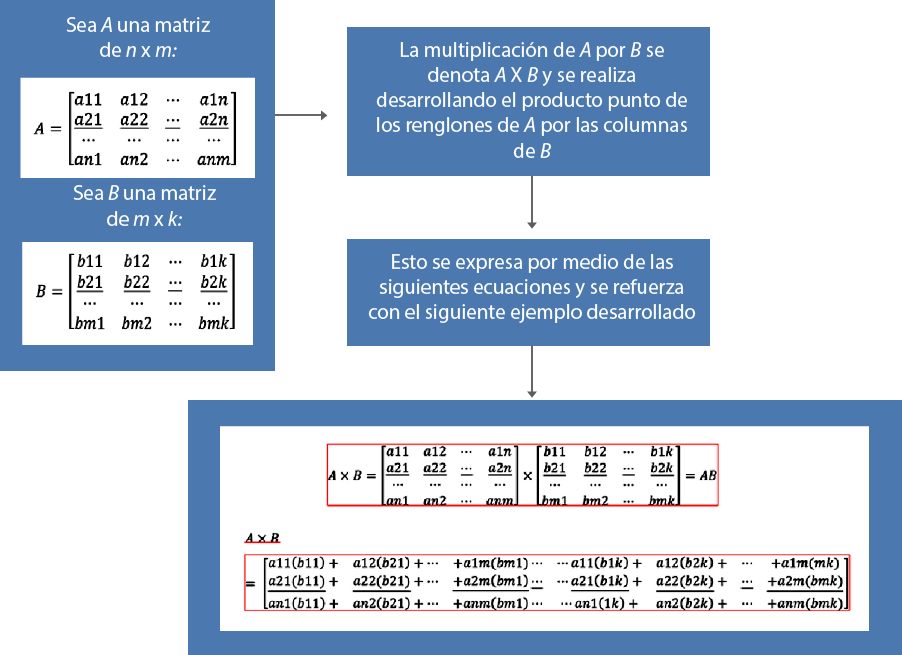
En esta unidad de aprendizaje, utilizarás las operaciones que pueden realizarse con matrices: suma, resta, multiplicación por un escalar y multiplicación e inversión de matrices. Dichas operaciones te permitirán modelar y solucionar los problemas.

(s. a) (2012). Cálculos [fotografía]. Tomada de https://www.flickr.com/photos/photography_lcbm/7409221800/