Introducción
Las matrices son una herramienta muy útil para expresar y discutir problemas que surgen en la vida real. En los negocios, a menudo es necesario calcular y combinar ciertos costos y cantidades de productos, situaciones que suelen expresarse a través de las tabulaciones o herramientas que permiten representar y relacionar fácilmente diferentes tipos de datos; sin embargo, esta capacidad de visualización no siempre rinde en una mecanización útil para desarrollar métodos de análisis.
Afortunadamente, para estas situaciones, el álgebra aporta ciertos recursos que hacen posible representar y trabajar las diversas estructuras tabulares a través de una metodología matemática más clara, fácil y rápida de operar, la cual se denomina matriz.
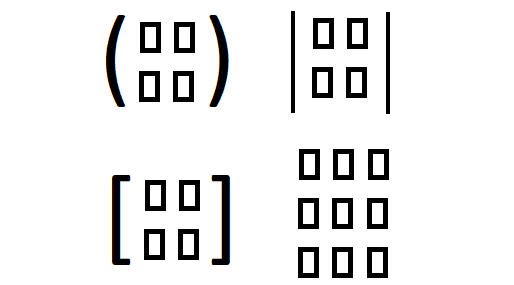
Matrices