Integración
Como ya se mencionó, la primera intención de la integración de una función es encontrar su primitiva; ahora, es necesario encontrar la regla de correspondencia para lograr ese objetivo.
A diferencia de la derivación de funciones, la cual cuenta con el método de los cuatro pasos para determinar la derivada de una función, aquí no existe un método general para obtener la integral de una función. ¿Qué hacer para integrar una función? Considera el siguiente caso:
Sin perder de vista que la tarea es encontrar la primitiva de la función (3.1), como un primer paso se observa la figura que muestra las reglas de derivación de una función, lo cual se ilustra a continuación:

Reglas de derivación
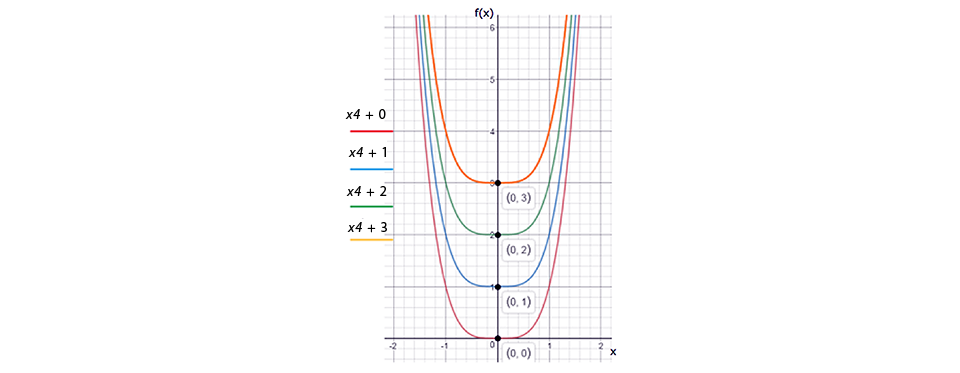
Al comparar la ecuación (3.1) con las reglas mostradas en los diferentes incisos, puedes notar que hay una relación entre la regla “h” y la ecuación (3.1); entonces, para obtener la primitiva no se requiere despejar la regla “h” de manera algebraica, sino realizar en sentido contrario las acciones indicadas en ella. Esto quiere decir que, en este caso, a la función “x3” le debes sumar 1 en el exponente, ya que originalmente se lo restaste. A su vez, debes dividirlo entre el valor de este nuevo exponente para que, al derivar, arroje la función derivada “f(x)”. Al realizar las acciones indicadas, resulta lo siguiente:
1. Potencia de la primitiva: 3 + 1 = 4
2. Coeficiente de la primitiva = 4
3. Primitiva F(x) = x4 / 4 (3.2)
Para comprobar que lo realizado es correcto, ahora derivarás “F(x)” para obtener “f(x)”. Al aplicar la regla “h”:
| d F(x) / dx = mxm-1 = 4x4-1 / 4 = 4x3 / 4 = x3 (3.3) |
Observa en la ecuación (3.3) que, efectivamente, la función (3.2) es la primitiva de la función (3.1). Además de comprobar la relación entre las ecuaciones (3.1) y (3.2), nota que el procedimiento es algo complejo, ya que debes realizar una redacción del procedimiento inverso antes de aplicarlo correctamente; por ello, existen una gran cantidad de tablas de integración que se obtienen al proponer funciones “tipo” y asociarlas a sus respectivas entradas en las tablas de derivación; de esta forma, es posible obtener las funciones primitivas.
A continuación, se muestra una pequeña tabla de integrales para funciones algebraicas:
a) ∫um dx = um+1 / m + 1 + C “C” es una constante
b) ∫ dx / x = ln |x| + C “C” es una constante
c) ∫ax dx = (ax / ln a) + C “C” es una constante
d) ∫ex du = ex + C “C” es una constante
e) ∫ k dx = kx + C “k” y “C” son constantes
Tabla 1. Integrales de funciones algebraicas