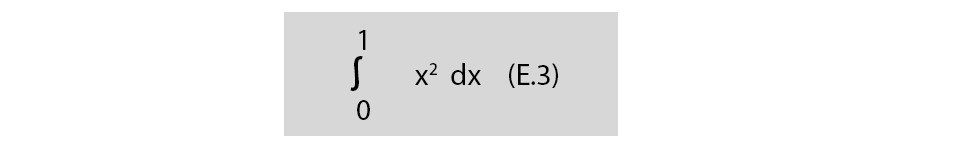Métodos de Integración

Unidad de Apoyo para el Aprendizaje

Iniciar

Introducción

¿Cómo integrar una función mediante la obtención de funciones equivalentes?

Para las operaciones algebraicas, existe un algoritmo que permite obtener el resultado deseado; en el cálculo diferencial, la derivada posee su propio procedimiento a través del método de los cuatro pasos. Sin embargo, la integración de funciones no cuenta con un algoritmo único; “aunque se sabe que la integral de una expresión diferencial dada existe, puede ser imposible obtenerla en términos de funciones conocidas” (Granville, 1963).

Esta condición conlleva la necesidad de contar con diversas estrategias que ayuden a determinar la antiderivada; en algunos casos, los métodos de integración ofrecen una de las alternativas que permiten encontrar una solución exacta. Su relevancia se debe a que brindan la posibilidad de trasformar ciertas expresiones matemáticas en expresiones algebraicas equivalentes que pueden ser ubicadas en una de las múltiples tablas de integración para integrar la función estudiada de manera precisa. En este tema, conocerás algunas de estas opciones que ayudan a obtener de forma sistemática la integral de una función para algunos tipos de expresiones matemáticas.





El estudio de este tema te permitirá:

  • Realizar la integración de algunos tipos de funciones, a través de transformaciones algebraicas.
  • Detallar algunas estrategias de conversión y simplificación para obtener funciones equivalentes y advertir el papel de las tablas de integrales en la determinación de funciones primitivas, las cuales son un recurso definitivo para responder a diversos problemas relacionados con el cálculo integral.
  • Determinar el área bajo una curva por medio de la regla de Barrow.

Integración por partes


En la búsqueda de la resolución de integrales, se recurre a diversos medios e incluso a las reglas de derivación. En el planteamiento de propiedades para la derivación de funciones, se encuentra una que versa sobre la multiplicación de dos funciones y señala que, cuando se deriva el producto de éstas, el resultado se obtiene por el producto “cruzado” de cada función involucrada con la derivada de la otra función. Esto se muestra a continuación:

d(uv) / dx = u d(v) / dx + v d(u) / dx; “u” y “v” son funciones de “x”     (e.1)

Si se busca aplicar la integración de funciones a (e.1), se puede expresar de la siguiente manera:

∫ f(x) (dx)    (e.2)

Al aplicar (e.2) a la ecuación (e.1) y hacer que f(x) = u(x) v(x), de manera sintética “uv”:

∫ (d(uv)/dx) (dx)= ∫u (d(v)/dx)(dx) + ∫v (d(u)/dx)(dx)    (e.3)

Al ser “dx” un término algebraico y encontrarse en numerador y denominador, (e.3) se simplifica de la siguiente manera:

∫ d(uv) = ∫u d(v) + ∫v d(u)    (e.4)

Al despejar en (e.4) el primer término después del signo de igual, se tiene lo siguiente:

∫u d(v) = ∫ d(uv) - ∫v d(u)    (e.5)

Si se recuerda que la derivación e integración son funciones inversas, se pueden simplificar en (e.5), lo que implica la eliminación de la integral y derivada indicadas de la siguiente forma:

∫ d(uv) = uv    (e.6)

Por (e.6), la expresión (e.5) se resume como sigue:


∫u d(v) = uv - ∫v d(u)    (e.7)

El objetivo de la expresión (e.7) es obtener una expresión más fácil de integrar; entonces, al aplicar el método propuesto en la ecuación original con el producto de dos funciones, ésta debe descomponerse en dos expresiones. Una de ellas no requiere integración (el término “uv”) y la otra debe ser más directa de resolver, ya sea porque algebraicamente se simplifica o la entrada de la función compuesta es inmediata en las tablas integración convencionales.

Con el fin de ilustrar el procedimiento que debe realizarse en la aplicación de este método, se propone el siguiente ejemplo.

Ejemplo 1. Integrar la siguiente ecuación:


f(x) = xex;    (E.1)

Al observar la ecuación (E.1), se busca su “entrada” en la siguiente tabla de integración:


Tabla de integración

Tabla 1. Algunas integrales de funciones algebraicas


La única entrada que tiene un componente parecido se encuentra en el inciso “d” de la tabla; sin embargo, no es posible aplicarla debido a que difieren por el factor “x” (E.1). Se aplica el método de integración por partes; se empieza por el lado izquierdo de (e.7):

∫u d(v) = ∫xex dx

Pulsa las flechas para avanzar y retroceder.

Previous Next

Integración por descomposición en fracciones


Entre los tipos de funciones susceptibles de simplificarse se encuentran los cocientes de polinomios, representados de la siguiente manera:

H(x) = f(x) / g(x), donde f(x) y g(x) son polinomios de grados “n” y “m”

Recuerda que un polinomio es una expresión matemática que posee la siguiente forma:

P(x) = anxn + an-1xn-1 + …a1x + a0    (11)
Donde “ai” son constantes y “ni” son números naturales

Las expresiones del tipo “H(x)” se clasifican como funciones propias, denominadas como “Hp(x)” si el grado del polinomio “f(x)” es menor que el grado de “g(x)”, e impropias, denominadas como “HI(x)” si el grado de “f(x)” es mayor que el de “g(x)”. En la teoría algebraica de este campo se sabe lo siguiente:


a) Toda función racional impropia “HI(x)” se puede expresar, en teoría, como la suma de un polinomio “P(x)” y una función propia “HP(x)”:

HI(x) = P(x) + HP(x)    (e.8)

b) Toda función racional propia “HP(x)” se puede expresar, en teoría, como suma de funciones simples con denominadores “g(x)” de la forma “(ax + b)n” y “(ax2 + bx + c)n”, donde “n” es un número entero y positivo:

HP(x) = A / (ax±b) + … + N / (ax±b)n + Ax + B / (ax2 + bx + c) + … + Mx + B / (ax2 + bx + c)n    (e.9)

Al revisar los incisos anteriores se observa que, a partir del primero (“a”), hay un polinomio más una función propia donde P(x) es el precedente, sujeto de integración directa o por medio de las tablas de integrales para funciones algebraicas; para ambos incisos (“a” y “b”), hay una parte relacionada con una función propia.

Para la simplificación de las expresiones propias “HP(x)”, se parte de la forma del denominador y pueden hallarse cuatro diferentes enfoques de solución que pueden revisarse con mayor amplitud en la bibliografía; en este tema, sólo se ejemplificará la simplificación que ofrece la técnica de integración por descomposición de fracciones para un caso específico. La finalidad de esto es mostrar las bondades de aplicación de esta metodología.

Ejemplo 2. Integrar la siguiente expresión:


∫ dx /(x2 – 4) dx    (E.2)

Pulsa las flechas para avanzar y retroceder por el procedimiento.

Previous Next

Es importante resaltar que el esfuerzo algebraico realizado en el desarrollo de este método tiene su recompensa en el hecho de poder transformar una expresión que no se puede integrar directamente en un par de expresiones equivalentes que son integrables a través de las tablas básicas de integración para obtener la solución exacta de la integral planteada (E.2.13). Cabe recordar que la interpretación de cada resultado obtenido depende del contexto de donde proviene el problema abordado.


Integral definida


Como se revisó en la interpretación geométrica de la integración de funciones, la integral de una función se asocia con la determinación del área bajo una curva. Por esta razón, es necesario identificar el procedimiento a través del cual se puede evaluar. Esta situación se define por medio de la denominada regla de Barrow, también conocida como teorema fundamental del cálculo integral, la cual dice que el área bajo una curva “f(x)” se puede determinar a partir de la evaluación de su función primitiva “F(x)” en un par de valores “a” y “b” que determinan una región de interés “(a,b)” en un problema analizado; matemáticamente, se enuncia de la siguiente manera:





Y puede ser ilustrado con la siguiente figura:


Gráfica que representa el área bajo una curva

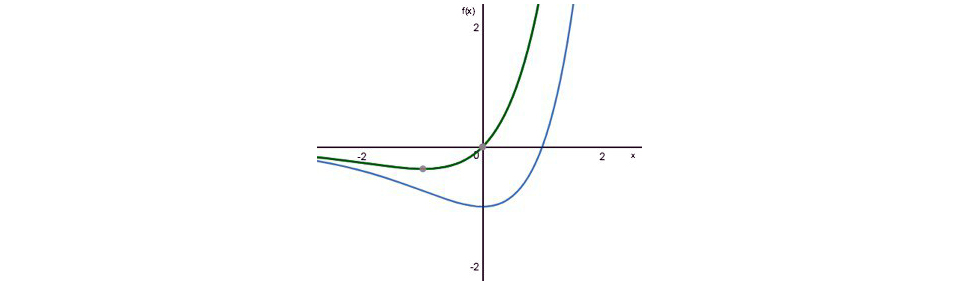
Interpretación geométrica del área bajo una curva, evaluada a través de los parámetros que indica la regla de Barrow: “(a,b)” definen una región en el plano, “f(x)” es la curva cuya superficie requiere definirse en la zona declarada y “F(x)” es su primitiva, a través de la cual se determina tal área


La expresión (e.10) muestra la importancia de obtener la primitiva “F(x)” de la función “f(x)”, ya que de forma simple, por la evaluación de un par de valores en F(x) y su diferencia, se puede resolver un problema complejo que dio origen al cálculo diferencial.

La expresión (e.10) se denomina integral definida, ya que determina de manera precisa el valor de un parámetro, es decir, el área bajo la curva de una función “f(x)”; en esta misma ecuación (e.10), se observa que la constante de integración “C” de la integral indefinida no aparece. Esto se debe a que, al realizarse la diferencia de las evaluaciones de la primitiva, la constante se anula, como se muestra a continuación al retomar la expresión de la integral indefinida:


∫ f(x) (dx) = F(x) + C    (e.11)

Al evaluar el lado derecho de (e.11) para los valores “b” y “a”:

F(b) + C    (e.11a)
F(a) + C    (e.11b)

Se toma la diferencia entre (e.11a) y (e.11b):

F(b) + C – (F(a) + C) = F(b) - F(a) + C – C = F(b) – F(a)    (e.11c)

Esto confirma que, para evaluar el área bajo “f(x)” a través de la regla de Barrow, la constante de integración no es necesaria, como lo indica la ecuación (e.10). Para consolidar la parte operativa del concepto, se muestra el siguiente ejemplo.

Ejemplo 3. Determinar el área bajo la curva “x2” en el intervalo (0,1) indicada por la siguiente integral definida:




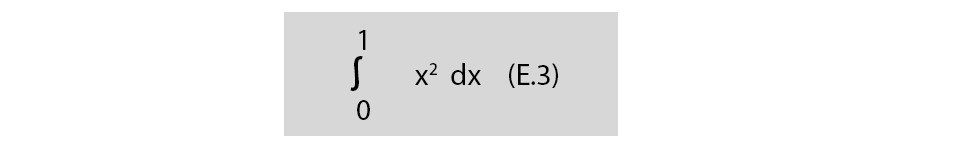
De acuerdo con la regla de Barrow, es posible determinar el área a través de la primitiva “F(x)” correspondiente a (E.3), la cual se obtiene al aplicar el inciso “a” de la tabla de integración 1:

∫um dx = um+1 / m + 1 + C    (T1.a)

Se aplica (T1.a) en (E.3):


∫ x2 (dx) = x3 / 3 + C = F(x)    (E.3.1)

Y el área pedida es la siguiente:

F(b) - F(a) = F(1) - F(0) = (1)3 / 3 – (0)3 / 3 = 1 / 3 u2    (E.3.2)

De esta manera, es posible determinar el valor del área bajo la curva (“u2” indica unidades de área) en el intervalo solicitado.


Representación gráfica del área bajo la curva del ejemplo 3.

Interpretación del área bajo la curva correspondiente al ejemplo 3, determinada por medio de la ecuación (E.3.1)


Conclusión


Como se comentó anteriormente, la necesidad de resolver una integral no es una curiosidad matemática; la antiderivada como función inversa y la interpretación geométrica del área bajo una curva, con la posibilidad de evaluarla mediante la regla de Barrow, ayudan a resolver una gran variedad de problemas como la determinación del coeficiente de desigualdad para distribución de ingreso, la evaluación del superávit consumidor-productor, la determinación del centro de gravedad, el valor promedio de una función, entre otros casos prácticos. De esta manera, la necesidad de obtener la primitiva de una función es imperante para dar respuesta a las interrogantes relacionadas.

Sin embargo, al no existir un algoritmo general para realizar la integración, se requiere utilizar los diversos recursos disponibles en el álgebra y la geometría, entre otras ramas de esta ciencia, para transformar expresiones matemáticas complejas a formas equivalentes más manejables, es decir, que puedan identificarse para su solución en las diversas tablas de integración. Es aquí donde los métodos de integración toman su justa medida de aplicación.



El cálculo integral está presente de manera sutil en una variedad de escenarios de la vida cotidiana; conocer la forma en que esto ocurre permite aprovechar al máximo el potencial de análisis que ofrece esta disciplina a través de sus recursos matemáticos.

Actividad de aprendizaje 1. Aplicaciones de la integral: métodos de integración y determinación del valor promedio de una función

Existen diversos parámetros de interés en distintos campos de las ciencias y la tecnología que versan sobre valores equivalentes asociados a una superficie o volumen; de esta manera, se hallan conceptos como el centro de masa o el valor promedio de una función, cuya definición los relaciona con procesos de integración.

En esta actividad, analizarás los enunciados que se te presentan y seleccionarás el método de integración para resolver algunos ejercicios.

Lee los siguientes enunciados y determina si son verdaderos o falsos al pulsar el alveolo correspondiente. Al finalizar, podrás conocer tu desempeño.


Autoevaluación. Métodos de integración en la obtención de funciones equivalentes

La integración es una operación matemática sin un procedimiento único de realización; por ello, es importante conocer las alternativas más comunes para obtener las expresiones primitivas correspondientes, lo cual ayudará a resolver los problemas asociados al cálculo integral. En esta actividad, analizarás los enunciados que se te presentan sobre los métodos de integración y asociarás el concepto al que se hace alusión.

Revisa los siguientes enunciados y elige la opción correspondiente para cada uno. Al terminar, podrás conocer tu desempeño.

Fuentes de información

Básicas

Bibliografía


Ayres, F. (1980). Cálculo Diferencial e Integral. México: McGraw-Hill.

Granville, W. (1963). Cálculo Diferencial e Integral. México: Unión Tipográfica Editorial Hispano-Americana.

Luthe, R., Olivera, A. y Schutz, F. (1984). Métodos numéricos. México: Limusa.


Sitios electrónicos


Wikipedia. (s. f.). [Entrada: Isaac Barrow]. Consultado el 7 de noviembre de 2017 de https://es.wikipedia.org/wiki/Isaac_Barrow

Wikipedia. (s. f.). [Entrada: Teorema fundamental de cálculo]. Consultado el 7 de noviembre de 2017 de https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo


Complementarias

Bibliografía

Granville, W. (1963). Cálculo Diferencial e Integral. México: Unión Tipográfica Editorial Hispano-Americana.


Cómo citar